Plamen Antonov's Pages/Math/Goldbach calculator

My Goldbach calculator

An old and still unsolved mathematical problem

No, it is only partially mine. The original idea and Method 1 algorithm belong to my friend Ivan here: Goldbach's Conjecture. I only implemented it in Javascript and added another (slower) method.

Named after German mathematician Christian Goldbach, who formulated it June 7th, 1742, Goldbach's conjecture is one of oldest yet unsolved problems in number theory and in mathematics at all. It says: Every even integer, greater than 2, is a Goldbach number, i.e. a number that can be expressed as a sum of two primes. That was called a Goldbach partition. Examples are: 4 = 2 + 2; 6 = 3 + 3; 8 = 3 + 5; 10 = 5 + 5 or 10 = 3 + 7; 12 = 5 + 7; 14 = 7 + 7 or 14 = 3 + 11.

Notes:	1.	As this calculator is Javascript based, if number entered is too big, and depending on computer speed, your browser might issue messages offering to abort the script. Obviously in that case not all expressions will be calculated;
	2.	This calculator doesn't work with FireFox (but does with Internet Explorer, Opera, and Chrome) due to some unexplored Javascript and forms behavior;
	3.	Javascript runtimes, calculated by the code itself, are very inconsistent. They give a real idea how long the code was run only if relatively big numbers are processed thus the runtime is greater.

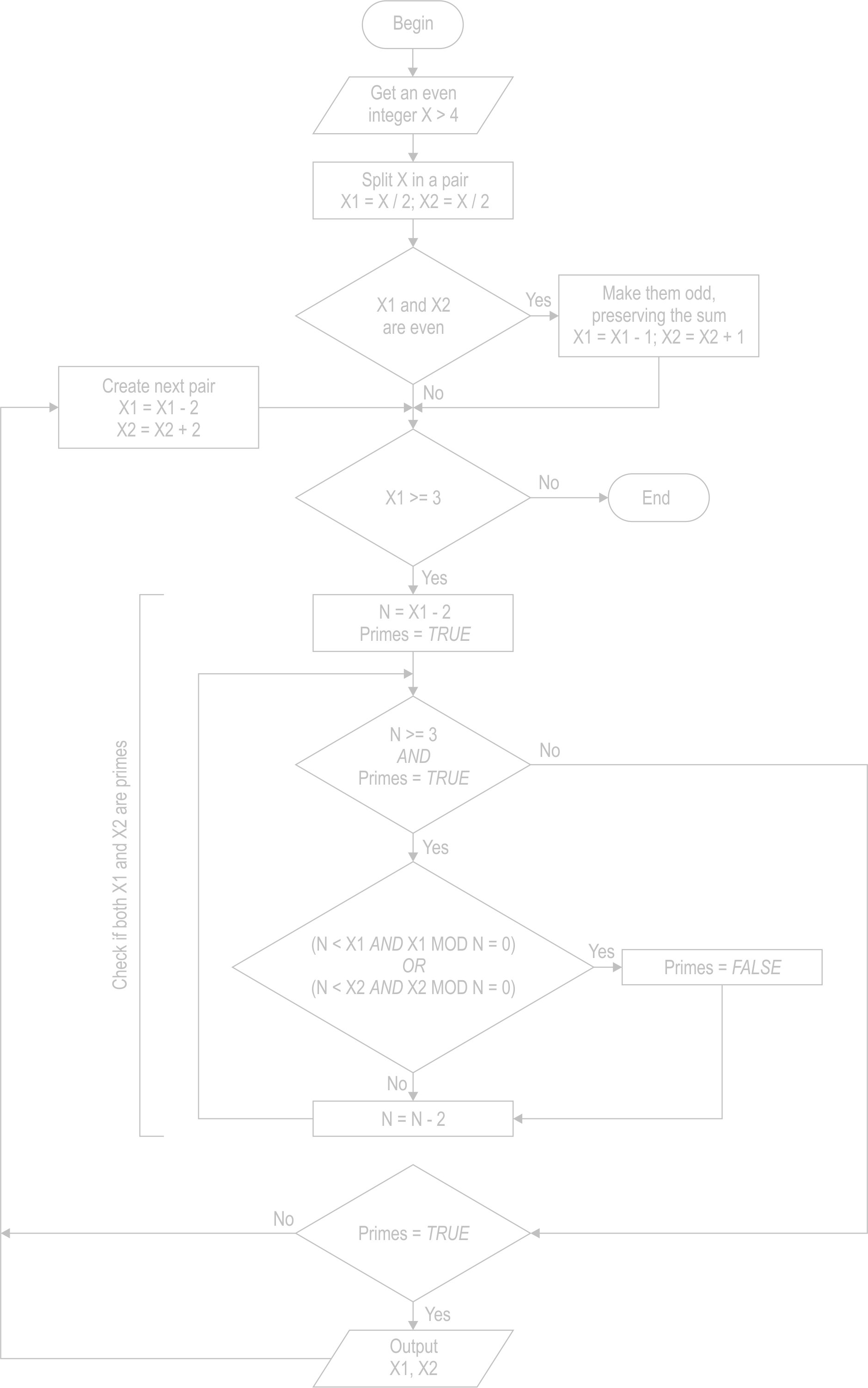
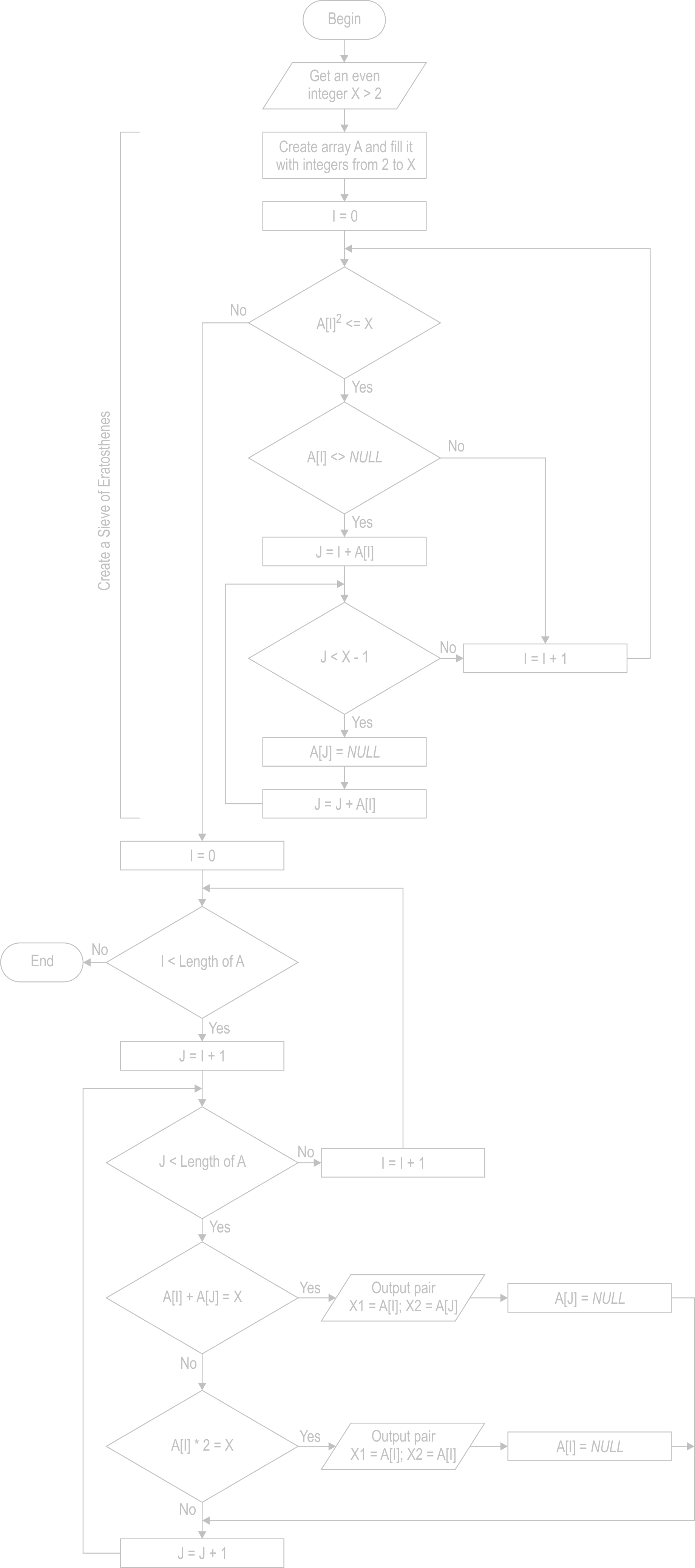
Comparing Method 1 with Method 2, which is yet another "Sieve of Eratosthenes" method, results in the following: Method 1 is memory-efficient as no intermediate data is stored thus the integer expanded could be (theoretically) unlimited; Method 2 stores intermediate data (Eratosthenes sieve) so largest number expandable is limited by the memory available, but in difference to Method 1 is capable of processing 4 = 2 + 2. Method 2 is significantly slower than Method 1 due to the bigger amount and complexity (multiplication) of calculations. Of course current Javascript implementation with all limitations, implied by web browsers, has more or less illustrative purpose. That's why the code isn't optimal for speed, but kept clear and easier to understand.

Method 1 and Method 2 algorithms in their current implementation, and the corresponding Javascript code fragmens:

Method 1

...get x >= 4...
x1 = x / 2;
x2 = x / 2;
if (x1 % 2 == 0){
   x1--;
   x2++;
}
while (x1 >= 3){
   n = x2 - 2;
   primes = true;
   while (n >= 3 && primes){
       if ((n < x1 && x1 % n == 0) || (n < x2 && x2 % n == 0)) {
           primes = false;
       }
   n -= 2;
   }
   if (primes){
       ...output x1, x2...
   }
   x1 -= 2;
   x2 += 2;
}

Method 2

...get x >= 2...
a = new Array(x - 1);
for (var i = 2; i <= x; i++){
   a[i - 2] = i;
}
i = 0;
while (a[i] * a[i] <= x){
   if (a[i] != null){
      for (var j = i + a[i]; j < x - 1; j += a[i]){
         a[j] = null;
      }
   }
   i++;
}
for (var i = 0; i < a.length - 1; i++){
   j = i + 1;
   while (j < a.length){
      if (a[i] + a[j] == x){
         ...output x1 = a[i], x2 = a[j]...
         a[j] = null;
      }
      else if (a[i] * 2 == x){
              ...output x1 = a[i], x2 = a[i]...
              a[i] = null;
           }
      j++;
   }
}

□

An even integer , greater than 2 :		Can be expressed as sums of following pair(s) of primes: Pair count:
		Method 1:	Method 2:
	Runtime: